A Case For Investing in Tankers

Fergus Cullen - better known as Trader Ferg - talks about the unloved, unpopular tankers sector and why you should consider it for your next investment.
Our weekly show with Fergus Cullen – better known as Trader Ferg – makes a case for another unpopular, unloved sector: tankers. More specifically, Ferg is particularly interested in the tankers that move crude oil and refined petroleum products.
What are tankers and why are they so unloved? Tankers are massive ships that transport goods around the world. The business is cyclical and directly tied to the volatile oil & gas market, which has burned a lot of investors. Environmental concerns are another strike against oil tankers as their carbon footprint is huge.
Despite this, and despite his description of tankers as a “terrible business,” Ferg is enthusiastic about investing in this sector.
The Tanker Market
The oil tanker market, similar to the uranium and oil and gas market, is highly cyclical. It’s driven by boom-and-bust cycles: lots of tankers are ordered when times are good and companies take on loads of debt, then there’s a glut of tankers followed by a crash.
This played out in an unfortunate way for some in the beginning of 2020. People who got involved with tanker investing in early 2020 expecting a storage crisis that would cause tanker rates to skyrocket, got burned. Oil demand plummeted when the COVID-19 pandemic hit, resulting in a surplus of oil and lack of storage, shortly followed by global production cuts.

Types of Tankers
There are several varieties of crude oil tankers:
- Coastal tankers (very small capacity)
- Aframax (650,000 barrel capacity)
- Suezmax (1 million barrel capacity)
- Very Large Crude Carriers (1.9–2.2 million barrel capacity)
- Ultra-Large Crude Carriers (2–3.7 million barrel capacity).
The market is similar between all tankers, so Ferg focuses on the Very Large Crude Carriers (VLCCs), which carry refined petroleum products like jet fuel, petrol and diesel. VLCCs are the workhorses of the tanker market. There are 804 VLCCs in the world, along with 668 Aframaxes and 570 Suezmaxes.

The tanker industry is seasonal and generally ramps up in the winter (Q4 and Q1). The majority of the population is in the northern hemisphere and the most oil is moved during the colder months.
Tanker pricing is essentially a day rate. Rates are determined by the daily break-even (the ship’s OpEx), debt requirements, interest, G&A and maintenance CapEx. Tanker day rates are typically somewhere between US$15,000–25,000. Rates increase according to demand – during the oil storage shortage in 2020, when oil had to be stored in ships floating offshore, some companies were making US$100,000–200,000 in day rates.
Special surveys
Tankers are made in shipyards and it usually takes 2–3 years to build them, depending on the current backlog. The industry is highly regulated, requiring tankers to go through multiple special surveys roughly every 5 years. During the first special survey, the pipes and linings of the tank are inspected to make sure there are no leaks, at a cost of US$1.5 million.
The second special survey, at 10 years of life, costs US$2 million and the third (at 15 years of life) costs US$2.5 million. After the 15 year mark, surveys are required every 2.5 years, at increasing costs, although most tankers don’t make it to year 20. And this doesn’t even include the ballast water treatment costs, which are US$1.5 million each year.
By 15 years of life, the cost of the surveys plus maintenance and repair costs are hard to justify. Most tankers of this age are scrapped for steel.

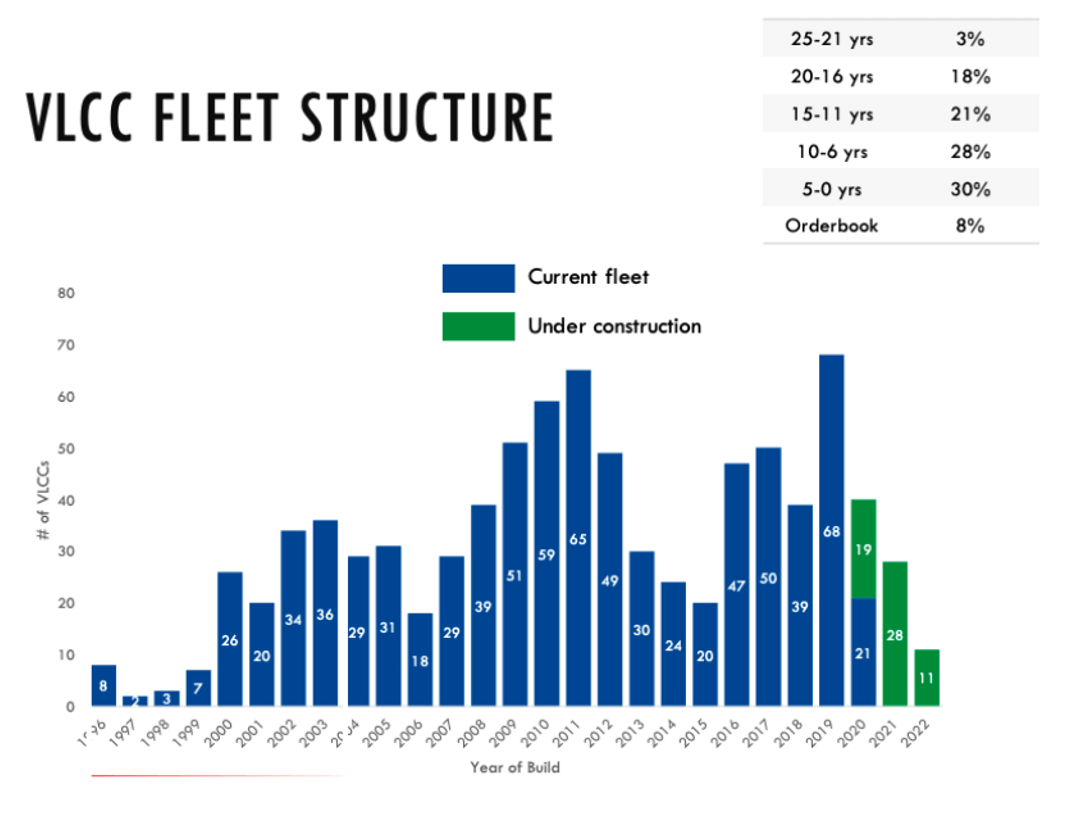
The current fleet structure gives an idea of how many tankers will be scrapped in the near future. Twenty-seven percent of the tankers in the current Suezmax fleet are nearing the scrapping age, and 18% of the VLCC fleet will likely be scrapped within the next 4 years. Three percent of the current VLCC fleet is over 21 years of age and will likely be scrapped immediately.
However, the current orders are only 10% of the Suezmax fleet and 8% of the VLCC fleet. With an average yearly scrapping rate of 5% of the fleet, this means 40 VLCCs need to be replaced each year. Current VLCC outlook shows a VLCC deficit of 12 tankers in 2021 and 29 in 2022, with no tankers scheduled to be introduced in 2023.
If shipping rates and demand are low, like they are now due to the COVID-19 pandemic, it’s more likely that ships will be scrapped instead of surveyed and maintained. The shipping market is heavily dependent on the oil market and is constructed around 100 million barrels per day capacity.
Unless oil demand picks up again, Ferg predicts the scrapping rate could be a lot worse–and that could be a good thing for investors.
IMO Regulations
Tanker order rates are currently at a 23 year low. Why? It’s a bear market and companies that are low on cash don’t want to place new orders. Another factor at play is the new International Marine Organization (IMO) regulations. IMO 30 regulations require a 40% reduction in carbon intensity of international shipping by 2030 and a 70% reduction by 2050.
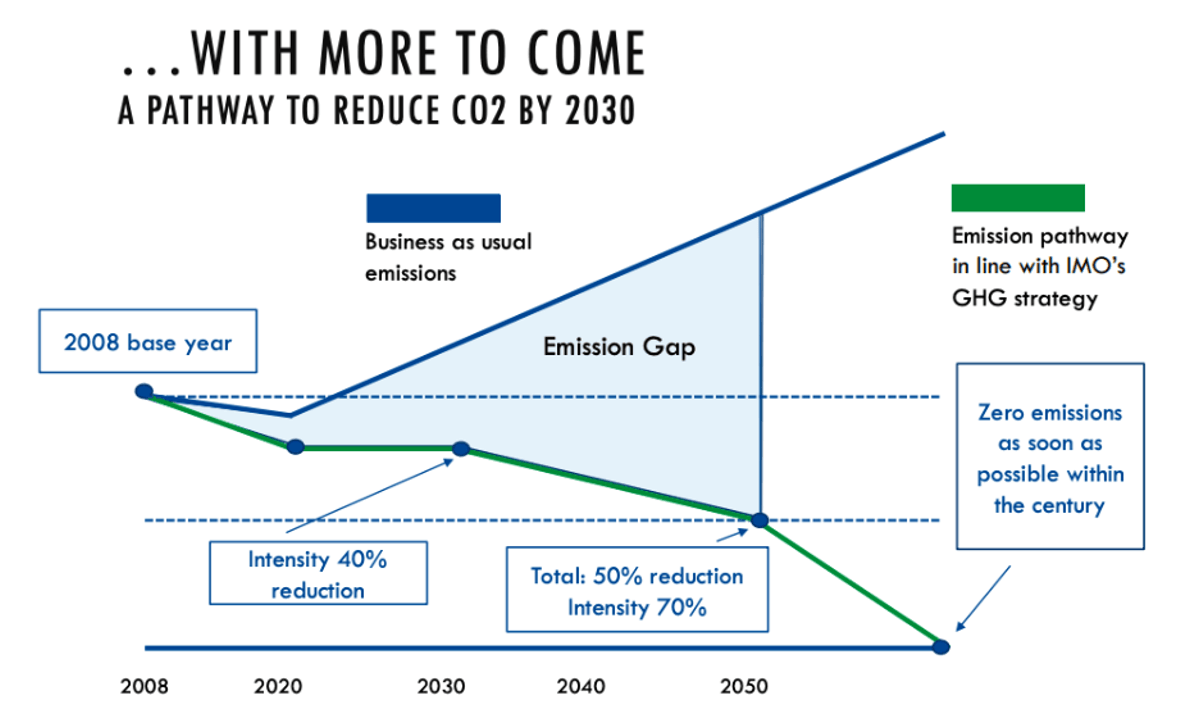
The current regulations (IMO 20) required a shift from high-sulfur fuel to low-sulfur fuel. Tankers had to install scrubbers to remove pollutants or switch to low-sulfur fuel, both of which come at a cost.
IMO 30 guidelines will increase the environmental considerations required by shipping companies. However, the guidelines won’t be fully established until 2023, leaving tanker companies in a bind. There’s simply too much uncertainty for companies to build a US$100–$120 million tanker that may be obsolete within the next 10 years.
Low-Carbon Solutions – Is The Technology There?
In light of the new IMO 30 regulations, a few carbon-conscious solutions have been proposed. One option is using liquified natural gas (LNG) to fuel tankers. However, studies of LNG tankers only show a 9–12% reduction in emissions compared to current tankers. Nuclear power, which is used by navies around the world, isn’t being considered for tankers at the moment.
In an interview, Hugo De Stoop, CEO of shipping firm Euronav (NYSE:EURN), stated that ammonia or hydrogen have the potential as a new shipping fuel. However, neither ammonia or hydrogen-powered tankers exist as of yet. Norway is currently working on a hydrogen-powered cruise ship, due to be completed in 2023.
Norway is also working on an ammonia tanker. Viking Energy, owned by Eidesvik, will be retrofitted to run on an ammonia fuel cell system by 2024.
What’s the realistic environmental impact of using hydrogen or ammonia to power tankers on a global scale? Right now, the hydrogen that’s produced around the world is for 2 general purposes: petrochemical refining and producing ammonia.
The environmental impact is described as green, blue, or black/grey/brown.
- Black, Grey and Brown hydrogen production is CO2-intensive and releases CO2 into the atmosphere.
- Blue hydrogen involves capturing and burying CO2, which prevents it from being released into the atmosphere.
- Green hydrogen is produced from electrolysis, which splits hydrogen atoms from water (H2O) and involves no CO2.

Right now, only 4-5% of hydrogen is produced from renewables (green). The remaining 95% (brown) is produced from fossil fuels like coal, oil or gas via a process called steam reforming. Steam reforming involves splitting the CO2 off from natural gas and ultimately releases the same amount of emissions as running a tanker on fossil fuels.
The same goes for ammonia, which is produced from hydrogen. If hydrogen is produced from a carbon-intensive method, the resulting ammonia will be just as carbon-intensive.
Producing green hydrogen via renewable methods like electrolysis requires a huge amount of energy. Using electrolysis to produce the amount of hydrogen needed to current refining and ammonia needs would require 3,600 terawatt-hours. That’s equivalent to the entire European Union’s power needs. Unless there is a breakthrough with blue hydrogen, renewable hydrogen can’t power the current global fleet of tankers.
Future Outlook
Right now, the technology to power tankers with hydrogen exists, but on far too small a scale to produce the necessary tankers by 2023. The Norwegians are financing liquid hydrogen fuel cell ships, which are powered by a combination of hydrogen and battery storage. But by the time they are proven and built, which could take up to two years, it will be too late to fill the empty 2023 order book.
The cycle is similar to the uranium fuel cycle. It’s not enough for a utility company to sign a new contract - it takes 18–24 months for the fuel rods to be delivered. The tanker industry, under pressure to build new ships that will meet IMO regulations, needs to find a new fuel technology, prove it, and build the ships.
Ferg thinks tanker companies can agree on a new design by the end of the year, but the industry is far from producing the 40 VLCCs needed by 2023. He predicts that oil demand will return to normal levels by the end of this year. According to Ferg, increased demand will reduce available storage capacity and drive shipping rates through the roof.
Ferg’s Take for Investors
If oil demand recovers as predicted, current scrap rate and empty order books will result in a deficit of tankers. Ferg is taking a basket approach to investing in the tankers sector.

In particular, he likes 3 players: Euronav, DHT Holdings, and Teekay Tankers. Each company has got scale, and they’ve proven to have reasonable management. All three are pure-play tanker companies who have improved their books, paid fat dividends and paid down their debts over the course of the last year.
Euronav (NYSE:EURN) has 45 VLCCs and 25 Suezmaxes. Ferg has ranked Euronav as the Rolls Royce of the bunch. He says CEO Hugo De Stoop is level-headed and has played the tanker industry perfectly. The only downside is that they’re a bit conservative, so the upsides may not be as large as other companies.
DHT Holdings (NYSE:DHT) is in the middle of the three with 30 VLCCs. The average age of their fleet is 6.7–6.8 years and their market cap is under US$1 billion.
Teekay Tankers (NYSE:TNK) has one VLCC, a handful of LNG ships, 18 Aframaxes and 26 Suezmaxes. Financially, they’ve been a shining example of what tanker companies can do in good times. Their current market cap is US$380 million, down from US$450 million at the start of 2020.
Teekay earned a free cash flow of US$100 million in Q4/19, US$150 million in Q1/20, and US$200 million in Q2/20. This is equivalent to their entire market cap in a period of 3 quarters. Of course, Ferg points out that this is a rare feat, but a successful feat nonetheless.
If you want more leverage, look at Scorpio Tankers (NYSE:STNG). They have a fleet of product tankers that move refined products like jet fuel and petrol. Scorpio has more leverage, as Compared to Euronav and DHT, Scorpio has more leverage as their fleet is younger. Scorpio’s fleet’s average age is just shy of five years old, but note that product tankers have to be retired at 15 years of age.
Tankers are an unloved sector, but Ferg is still excited about them, so take note of his suggestions. With oil demand expected to recover and the current scrap rate, the empty order books, and upcoming IMO regulations, this sector is full of opportunity.
Analyst's Notes




Subscribe to Our Channel
Stay Informed











